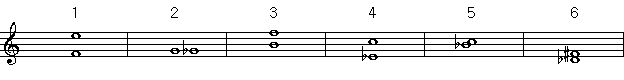7. 음정(Interval)

 1) 음정 : 음정이란 두 음사이의 거리(높이의 간격)을 말한다.

    ① 음정의 도수 계산하기 - 음정의 도수는 두음 중에서 낮은음부터 높은음까지의 계이름 갯수를 세어보면 된다.

       우선 <다장조>의 경우를 예로 들어보면,  

 2) 홑음정과 겹음정

    ① 홑음정 : 음정의 도수가 옥타브 안에 들어 있는 것(1도부터 8도까지의 음정)

    ② 겹음정 : 음정의 도수가 옥타브를 벗어난 것(9도 이상의 음정)

      겹음정을 홑음정으로 바꾸기  :   겹음정 - 7 = 홑음정

 3) 기본음정 (모든 음정을 계산할 때는 여기서부터 출발한다.)

                    위 표의 내용을 암기하는 것이 좋다.

 4) 음정의 성질 변화 : 음정을 이루는 두 음에 #, b, 등이 붙어 높이의 변화가 생기면 음정의 성질도 달라진다.

    설명 :

       완전음정인 1, 4, 5, 8도가 거리(간격)가 반음 늘어나면 증음정이되고,

                 완전1도 -> 증1도       완전4도 -> 증4도        완전5도 -> 증5도         완전8도 -> 증8도 

       완전음정인 1, 4, 5, 8도가 거리(간격)가 반음 줄어들면 감음정이 된다.

                 완전4도 -> 감4도       완전5도 -> 감5도        완전8도 -> 감8도

                (그런데 감1도라는 음정은 없다. 왜냐하면 완전1도는 두음의 높이가 똑같아서 간격이 0인 상태인데,
                     0보다 더 좁은 간격은 없기 때문이다.)

       장음정인 2, 3, 6, 7도가 반음 늘어나면 증음정이 되고,

                 장2도 -> 증2도          장3도 -> 증3도          장6도 -> 증6도           장7도 -> 증7도

       장음정인 2, 3, 6, 7도가 반음 줄어들면 단음정이 된다.

                 장2도 -> 단2도          장3도 -> 단3도          장6도 -> 단6도           장7도 -> 단7도

       단음정이 된 2, 3, 6, 7도가 또 반음 줄어들면 감음정이 된다.

                 단2도 -> 감2도          단3도 -> 감3도          단6도 -> 감6도           단7도 -> 감7도

       단음정이 된 2, 3, 6, 7도가 다시 반음 늘어나면 장음정이 된다.

                 단2도 -> 장2도          단3도 -> 장3도          단6도 -> 장6도           단7도 -> 장7도

 5) 음정 계산하기

     1) 먼저 낮은음에서 높은음까지의 계이름을 차례로 읽는다. 그때 계이름의 갯수가 그 음정의 도수가 된다.

     2) 그 음정의 계이름 사이에 반음이 몇 개 있는지 살펴본다.(미-파, 시-도 사이가 반음이다.)

     3) 외워두었던 기본음정과 반음수를 비교한다. 만약 기본음정보다 반음수가 많으면 그 음정은 오히려 반음 간격이
        줄어든 것이고(-), 반음수가 기본음정보다 적으면 오히려 반음이 늘어난 것이다(+).
        - (왜 그럴까? - 같은 도수에서 반음수가 더 많다는 것은 그대신 온음이 하나 빠져나갔기 때문이다.)
        따라서 음정의 성질 변화 표에서 도수와 간격의 변화를 살펴서 음정을 알아낸다.

     4) 만약 임시표(#, b, )가 붙어 있으면 이를 다시 계산해야 한다.
        만약 높은음이 올라가면 반음 늘어난 것이고(+), 낮은음이 올라가면 반음 줄어든 것이다(-).

        또, 높은음이 내려가면 반음 줄어든 것이고(-), 낮은음이 내려가면 반음 늘어난 것이다(+).

    <실습1>      

       우선 <다장조>에서

     <1번 문제>

         1. 낮은음에서 높은음까지의 계이름을 읽어보면 <미,파,솔,라> 4개음이다. 그러므로 도수는 4도이다.

         2. 여기에는 <미-파> 반음이 1개 있다.

         3. 기본음정 4도는 <완전음정>이고, 반음수가 1개인데 여기도 1개로 같으므로 이 음정은 <완전4도>이다.

     <2번 문제>

         1. 낮은음에서 높은음까지의 계이름을 읽어보면 <레,미,파> 3개음이다. 그러므로 도수는 3도이다.
         2. 여기에는 <미-파> 반음이 1개 있다.

         3. 기본음정 3도는 <장음정>이고 반음수가 0인데 여기는 반음이 1개 있으므로 반음 줄어든(-) 것이다.
            따라서 장3도가 줄어들어 <단3도>가 되었다.

     <3번 문제>

         1. 낮은음에서 높은음까지의 계이름을 읽어보면 <미,파,솔,라,시,도> 6개음이다. 그러므로 도수는 6도이다.
         2. 여기에는 <미-파, 시-도> 반음이 2개 있다.

         3. 기본음정 6도는 <장음정>이고 반음수가 1개인데 여기는 반음이 2개 있으므로 반음 줄어든(-) 것이다.
            따라서 장6도가 줄어들어 <단6도>가 되었다.

     <4번 문제>

         1. 낮은음에서 높은음까지의 계이름을 읽어보면 <파,솔,라,시> 4개음이다. 그러므로 도수는 4도이다.

         2. 여기에는 반음이 하나도 없다.

         3. 기본음정 4도는 <완전음정>이고, 반음수가 1개 인데 여기는 반음이 없으므로 반음 늘어난(+) 것이다.
            따라서 완전4도가 늘어나(+) <증4도>이다.

     <5번 문제>

         1. 낮은음에서 높은음까지의 계이름을 읽어보면 <레,미,파> 3개음이다. 그러므로 도수는 3도이다.
         2. 여기에는 <미-파> 반음이 1개 있다.

         3. 기본음정 3도는 <장음정>이고 반음수가 0인데 여기는 반음이 1개 있으므로 반음 줄어든(-) 것이다.
            따라서 장3도가 줄어들어 <단3도>가 되었다.
         4. 그런데 높은음에 #(올림표)이 붙어서 간격이 넓어졌다(+).
            따라서 단3도가 늘어나(+) 다시 <장3도>로 되었다.

     <6번 문제>

         1. 낮은음에서 높은음까지 계이름을 읽어보면 <미,파,솔,라,시,도,레> 7개음이다. 그러므로 도수는 7도이다.

         2. 여기에는 <미-파, 시-도> 반음이 2개 있다.

         3. 기본음정 7도는 <장음정>이고 반음수가 1개인데 여기는 2개 있으므로 반음 줄어든(-) 것이다.

            따라서 장7도가 반음줄어들어(-) <단7도>가 되었다.

         4. 그런데 높은음에 b(내림표)이 붙어서 간격이 좁아졌다(-).
            따라서 단7도가 줄어들어 <감7도>가 되었다.

    <실습2>      

       조표가 있는 경우                     

     <7번 문제>

         1. 낮은음에서 높은음까지의 라장조 계이름을 읽어보면 <도,레,미> 3개음이다. 그러므로 도수는 3도이다

         2. 여기에는 반음이 없다.

         3. 기본음정 3도는 <장음정>이고 반음수가 0이어서 반음수가 같으므로 <장3도>이다.

     <8번 문제>

         1. 낮은음에서 높은음까지의 라장조 계이름을 읽어보면 <레,미,파,솔,라,시> 6개음이다. 그러므로 도수는 6도이다.
         2. 여기에는 <미-파> 반음이 1개 있다.

         3. 기본음정 6도는 <장음정>이고 반음수가 1인데 여기도 반음수가 1개 있으므로 같은 <장6도>이다.
         4. 그런데 높은음에 (제자리표)가 붙어 있다. 이것은 조표에 붙어있는 #(올림표)를 제자리로 돌리는 것이므로
            반음 내리라는(-) 뜻이다. 따라서 장6도가 반음 줄어들어 <단6도>가 되었다.

     <9번문제>

         1. 낮은음에서 높은음까지의 내림마장조 계이름을 읽어보면 <미,파,솔> 3개음이다. 그러므로 도수는 3도이다.
         2. 여기에는 <미-파> 반음이 1개 있다.

         3. 기본음정 3도는 <장음정>이고 반음이 0인데 여기는 반음이 1개 있으므로 반음 줄어든(-) 것이다.
            따라서 장3도가 줄어들어 <단3도>가 되었다.

         4. 그런데 낮은음에 #(올림표)이 붙어서 간격이 좁아졌다(-). 따라서 단3도가 줄어들어(-) <감3도>가 되었다.

     <10번문제>

         1. 낮은음에서 높은음까지의 내림마장조 계이름을 읽어보면 <파,솔,라,시> 4개음이다. 그러므로 도수는 4도이다.

         2. 여기에는 반음이 하나도 없다.

         3. 기본음정 4도는 <완전음정>이고, 반음수가 1개 인데 여기는 반음이 없으므로 반음 늘어난(+) 것이다.
            따라서 완전4도가 늘어나(+) <증4도>이다.

         4. 그런데 높은음에 b(내림표)이 붙어서 간격이 좁아졌다(-). 따라서 증4도가 줄어들어(-) <완전4도>가 되었다.

     <11번문제>

         1. 낮은음에서 높은음까지의 가장조 계이름을 읽어보면 <라,시,도,레,미> 5개음이다. 그러므로 도수는 5도이다.
         2. 여기에는 <시-도> 반음이 1개 있다.

         3. 기본음정 5도는 <완전음정>이고 반음이 1개인데 여기도 반음이 1개 있으므로 <완전5도>이다.

         4. 그런데 낮은음에 (제자리표)가 붙어있다. 이것은 조표에 붙어있는 #(올림표)를 제자리로 돌리라는 뜻이므로

            반음이 내려간다. 따라서 간격이 넓어지므로(+) 완전5도가 늘어나(+) <증5도>로 되었다.

     <12번문제>

         1. 낮은음에서 높은음까지 가장조 계이름을 읽어보면 <시,도,레,미> 4개음이다. 그러므로 도수는 4도이다.

         2. 여기에는 <시-도> 반음이 1개 있다.

         3. 기본음정 4도는 <완전음정>이고 반음수가 1개인데 여기도 1개 있으므로 <완전4도>이다.

         4. 그런데 높은음에 (제자리표)가 붙어있다. 이것은 조표에 붙어있는 #(올림표)를 제자리로 돌리라는 뜻이므로

            높은음이 반음 내려가 간격이 좁아졌다(-). 따라서 완전4도가 줄어들어(-) <감4도>가 되었다.

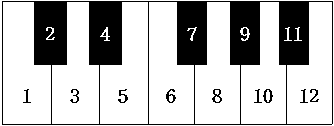
 6) 건반에서의 음정 비교

        먼저 <장3도>를 보면 낮은음이<도>이므로 건반 1번이고, 높은음이 <미>이므로 건반 5번이 된다.
          따라서 단순히 반음 건반 갯수로만 보면 1, 2, 3, 4, 5의 5개 건반이고,

       <단3도>를 보면 낮은음이 <미>이므로 건반 5번이고, 높은음이 <솔>이므로 건반 8번이 된다.
          따라서 단순히 반음 건반 갯수로만 보면 5, 6, 7, 8의 4개 건반이 되어 <단3도>가 <장3도> 보다 반음 건반 1개
          간격이 좁은 것이다.

 7) 음정의 자리바꿈  :  음정을 이루는 두 음 중 낮은음이 옥타브 위로 올라가거나, 높은음이 옥타브 아래로 내려오는
                         것을 말한다.

     <실습3>  다음 음정의 성질과 도수를 쓰시오.

답 알아보기